In How Not to Be Wrong: The Power of Mathematical Thinking, Jordan Ellenberg explores how math applies to everyday decisions, helping us avoid common logical errors. This blog highlights key lessons from the book, including the importance of statistical thinking, understanding probability, and recognizing patterns. Perfect for readers looking to improve decision-making skills and think critically in daily life, this insightful guide demonstrates that math is more than just numbers—it’s a way of seeing the world.
How Not to Be Wrong: The Power of Mathematical Thinking by Jordan Ellenberg teaches readers how mathematical thinking applies to everyday life. Here are 25 key lessons from the book:
1. Mathematics is Everywhere: Math isn’t confined to classrooms; it’s a tool that can be used to understand politics, economics, and daily decision-making.
2. Linear Thinking Can Mislead: Not all processes or systems in life grow linearly. Understanding this prevents false expectations and predictions.
3. Statistical Intuition: Numbers and statistics can deceive if you don’t know how to interpret them correctly. Learn to think critically about numbers.
4. The Importance of Outliers: Sometimes, outliers—those rare, unexpected cases—can teach us more than typical examples.
5. Survivorship Bias: We often focus on successes while ignoring failures, leading to distorted conclusions. Look for what’s missing.
6. Non-Zero-Sum Thinking: Not all situations are win-lose. Recognize when collaboration and cooperation create more overall value.
7. Correlation Doesn’t Equal Causation: Just because two things are related doesn’t mean one causes the other. Be careful with assumptions.
8. Expectation vs. Reality: We often expect more symmetry or fairness in life than actually exists. Math can help us better align expectations with reality.
9. Law of Large Numbers: Patterns emerge when looking at large enough sets of data. Small samples can mislead.
10. Bayesian Thinking: In decision-making, update your beliefs based on new evidence—much like how Bayes’ Theorem updates probabilities.
11. The Power of Averages: Averages can hide important details. For example, high-income inequality can lead to misleading average income statistics.
12. Counterfactuals Matter: Sometimes the most important information is what didn’t happen. Considering alternatives can sharpen understanding.
13. Conditional Probability: The likelihood of something happening depends on the conditions set. Understanding conditional probability refines our judgments.
14. Regression to the Mean: Extreme events or performances tend to be followed by more average outcomes. Don’t mistake this for a trend.
15. Coincidences Aren’t Always Special: Mathematically, unlikely events happen all the time. Don’t assign too much meaning to random coincidences.
16. Exponential Growth: Small, steady growth can lead to massive changes over time. This is often misunderstood when thinking about long-term processes like population growth or compounding interest.
17. Voting Paradoxes: Simple voting systems can sometimes produce unfair or illogical results. Math can reveal the weaknesses in these systems.
18. Risk vs. Reward: In complex situations, what appears as a high reward might carry disproportionate risk. Mathematical thinking helps evaluate trade-offs.
19. The Utility of Randomness: Randomness isn’t always bad. Sometimes introducing randomness can lead to better results in areas like decision-making and problem-solving.
20. The Monty Hall Problem: This famous probability puzzle shows that intuitive answers are often wrong. Always think critically before making decisions.
21. Game Theory: Understanding the strategies of others can influence your own decisions, leading to better outcomes.
22. Gambler’s Fallacy: The belief that past events influence future probabilities in independent events (e.g., flipping a coin) is a common error.
23. Math Helps Combat Bias: Recognizing cognitive biases is easier with mathematical thinking, as it imposes logical constraints on how we think.
24. Simpson’s Paradox: Trends that appear in different groups of data can disappear or reverse when the groups are combined, showing the complexity of interpreting data.
25. Mathematical Thinking Requires Practice: Just like any other skill, applying mathematical reasoning to real-life situations gets easier with practice. It’s about developing a mindset that questions assumptions and looks for underlying patterns.
Ellenberg’s book emphasizes that mathematical thinking is about recognizing patterns, avoiding common errors in reasoning, and making more informed decisions in everyday life.
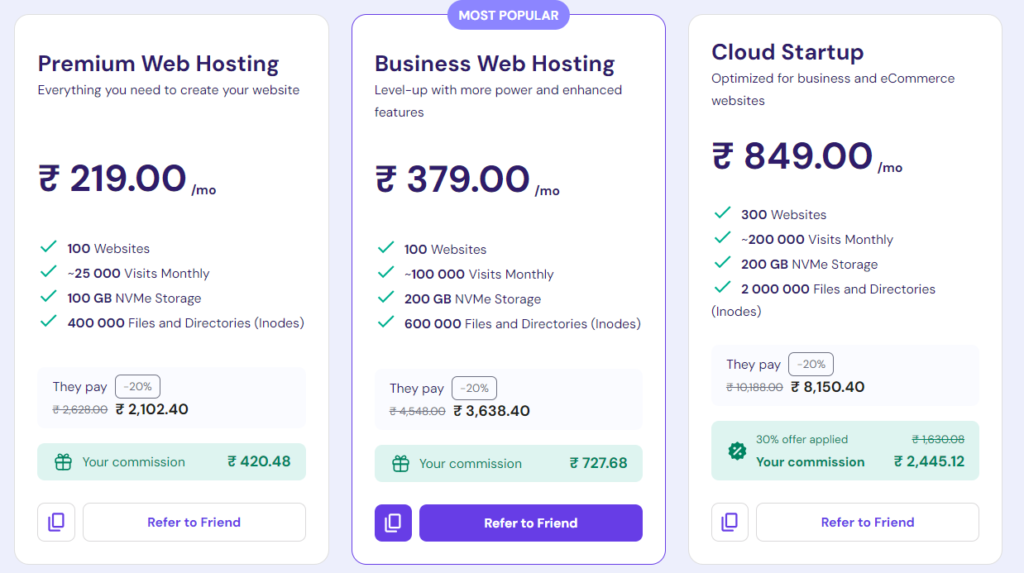
“Start Your Website Journey Today – Exclusive Hostinger Discounts!”